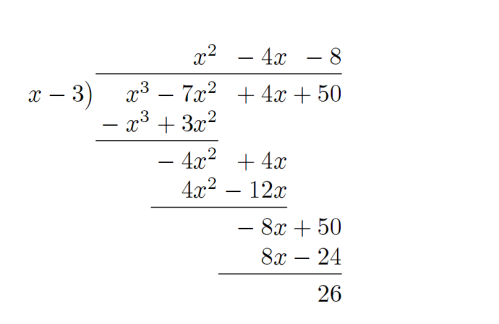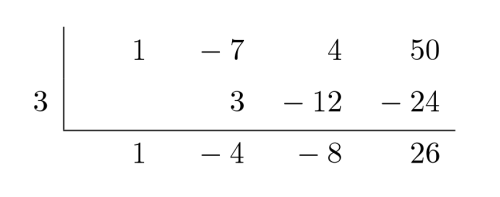Tampilkan postingan dengan label Matematika. Tampilkan semua postingan
Tampilkan postingan dengan label Matematika. Tampilkan semua postingan

Minggu, 11 Maret 2012

Aplikasi Persamaan Diferensial Orde satu


Quantcast
Dalam bagian ini kita akan bahas beberapa penerapan persamaan diferensial orde satu. Dalam kehidupan sehari-hari banyak fenomena yang dalam menyelesaikannya menggunakan persamaan diferensial orde satu. Contoh penerapan diferensial orde satu sering dijumpai dalam masalah pencairan atau pemekatan suatu cairan, masalah suku bunga bank, masalah pembelahan dan pertumbuhan sel, masalah dalam mekanika dan lain sebagainya.

Masalah Konsentrasi suatu cairan

Dalam sub bagian ini kita akan bahas masalah pemekatan dan pencairan suatu zat cair. Dalam masalah ini, kita akan menemukan suatu formula yang menyatakan jumlah dari substansi sebagai suatu fungsi dari waktu t, dimana jumlah ini akan berubah secara teratur setiap satuan waktu.

Contoh : 

Sebuah bak memuat 100 liter air. Karena suatu kesalahan 300 pon garam tertaburkan dalam bak yang mestinya diperlukan 200 pon. Untuk mengatasi masalah ini, dibuanglah air yang sudah bercampur garam dengan teratur 3 liter tiap menit. Dalam waktu yang sama ke dalam bak dimasukkan juga 3 liter air murni. Jika dijaga agar kondisi garam dalam bak merata setiap saat dengan diadakan pengadukan. Pertanyaan yang muncul adalah diperlukan berapa lama agar garam yang ada dalam bak sesuai yang diharapkan yaitu 200 pon?
untuk selengkapnya silahkan download disini !
Diposting oleh di Tidak ada komentar:
Label:

Soal Proyeksi Orthogonal

Soal Ujian Nasional Matematika kelas XII IPA
Diketahui vektor \vec{a}=2\vec{i}-4\vec{j}-6\vec{k} dan vektor \vec{b}=2\vec{i}-2\vec{j}+4\vec{k}. Proyeksi orthogonal vektor \vec{a} terhadap vektor \vec{b} adalah ….

Jawaban :
\vec{a}=2\vec{i}-4\vec{j}-6\vec{k}
\vec{b}=2\vec{i}-2\vec{j}+4\vec{k}
Proyeksi orthogonal vektor \vec{a} terhadap vektor \vec{b} saya misalkan e. Dengan rumus e=\dfrac{a.b}{|b|^2}b. Terlebih dahulu kita mencari nilai \vec{a}.\vec{b}.
\vec{a}\vec{b}=-12
|b|=\sqrt{2^2+(-2)^2+4^2}
|b|=\sqrt{4+4+16}
|b|=\sqrt{24}
|b|^2=24
e=\dfrac{\vec{a}\vec{b}}{|b|^2}\vec{b}
e=\dfrac{-12}{24}(2,-2,4)
e=\dfrac{-1}{2}(2,-2,4)
e=(-1,1,-2)
Jadi, Proyeksi Orthogonalnya adalah e=-\vec{i}+\vec{j}-2\vec{k}
Diposting oleh di Tidak ada komentar:
Label:

Penggunaan Polynom LaTeX Pada Pembagian Fungsi Polinomial

 Quantcast
Paket Polynom digunakan (di implementasikan) atau diaplikasikan untuk memanipulasi persamaan polinom (Polinomials). Antara lain Kita dapat mensetting polinomial pembagian panjang dan Pembagian Sintetik (Skema Horner), yang dapat kita tampilkan langkah demi langkah. Persoalan pertama dan aplikasinya adalah persamaan polinomial pada satu variabel dengan koefisien bilangan rasonal.

Donald Arseneau telah banyak berkontribusi dalam paket pada komunitas TeX. Khususnya dia mempublikasikan makro untuk pembagian panjang (Pembagian bersusun) pada comp.tex. tex juga telah terpublikasi dalam TGUBoat dan sebagai longdiv.tex pada CTAN.  Paket Polynom mengijinkan kita melakukan pekerjaan yang berhubungan dengan polinomial. Di Sini kita juga bisa memahami satu contoh dari skema Horner untuk pembagian sintetik.
Pada Algoritma Euclidean untuk menentukan satu pembagi terbesar dari dua polinomial, dan pada hal lain faktorisasi dari polinomial dengan paling banyak dua bilangan rasional bukan nol. Ini harus mencukupi bagi kebanyakan alat bantu.

Bagi anda yang sekarang sedang menyandang gelar sebagai guru SMA khususnya guru mata pelajaran matematika, mungkin paket ini cukup berguna untuk anda. Coba anda bayangkan saja jika kita harus menuliskannya dengan menggunakan Microsoft Word  maka kita akan merasa kesulitan dan akan memakan waktu yang cukup lama. Jadi, saya sarankan menggunakan \LaTeX dengan paket polynom merupakan saran yang pas dalam situasi yang cukup sulit ini.
Cara menggunakan paket ini adalah terlebih dahulu kita harus mendeklarasikan perintah berikut ini pada preambule:
\usepackage{polynom}
Jika anda belum memiliki paket tersebut silahkan dapatkan paketnya di ctan.org

Contoh Penggunaan Paket Polynom
P(x)=x^3 - 7x^2+ 4x + 50 adalah suku banyak x berderajat 3. Pembagian P(x) oleh x-3 dengan dua metode adalah sebagai berikut:
Pembagian Panjang
Gambar 1. Metode Pembagian Panjang
Dengan cara Horner diperoleh:
Gambar 2. Metode Horner
Jika di \LaTeX anda tidak perlu susah-susah menuliskannya. cukup dengan menuliskan perintah:
Untuk gambar pertama yaitu Pembagian Panjang anda cukup mengetikkan perintah:
$\polylongdiv{x^3-7x^2+4x+50}{x-3}$
Untuk gambar kedua yaitu Metode Horner anda cukup mengetikkan perintah
$\polyhornerscheme[x=3]{x^3-7x^2+4x+50}$
Cukup mudah bukan. Jika masih bingung silahkan baca artikel saya di suku banyak

Disadur Dari
Carsten Heinz and Hendri Adriaens. 2006. The Polynom Package Version 0.17.
Diposting oleh di Tidak ada komentar:
Label:

Dimensi Tiga - Jarak Titik Ke Bidang




Ada soal mengenai dimensi tiga. Dengan materi jarak titik ke bidang. Soal ini pernah masuk di Ujian Nasional Tahun 2011.

Diketahui kubus ABCD.EFGH dengan panjang rusuk a cm. Jarak C ke bidang AFH adalah ….

Jawaban:


Dari gambar diatas terlihat bahwa yang akan kita cari adalah jarak dari titik C ke titik P. OK langsung saja:
AC=\sqrt{AB^2+BC^2}
AC=\sqrt{a^2+a^2}
AC=a\sqrt{2}
Karena Nilai AC = a\sqrt{2} maka nilai FH juga a\sqrt{2} dan nilai EG juga a\sqrt{2} dan nilai EC adalah \dfrac{a}{2}\sqrt{2}. Sekarang kita akan mencari panjang AQ.
AQ=\sqrt{AE^2+EQ^2}
AQ=\sqrt{a^2+\left(\dfrac{a}{2}\sqrt{2}\right)^2}
AQ=\sqrt{a^2+\dfrac{a^2}{2}}
AQ=\sqrt{\dfrac{3}{2}a^2}
AQ=a\sqrt{\dfrac{3}{2}}
Sekarang kita tinjau Segitiga AQR.
\sin(A)=\dfrac{QR}{AQ}
\sin(A)=\dfrac{a}{a\sqrt{\dfrac{3}{2}}}
\sin(A)=\dfrac{1}{\sqrt{\dfrac{3}{2}}}
\sin(A)=\dfrac{2}{3}\sqrt{\dfrac{3}{2}}
Sekarang kita tinjau Segitiga APC.
\sin(A)=\dfrac{CP}{AC}
\frac{2}{3}\sqrt{\dfrac{3}{2}}=\dfrac{CP}{a\sqrt{2}}
CP=\dfrac{2}{3}\sqrt{\dfrac{3}{2}} x a\sqrt{2}
CP=\dfrac{2}{3}a\sqrt{3}
Jadi, Jarak titik C ke bidang AFH adalah \dfrac{2}{3}a\sqrt{3}

Diposting oleh di Tidak ada komentar:
Label:
Langganan: Postingan (Atom)